수학이라고 하면 대부분 딱딱하고 어려운 공식만 떠오르기 쉽죠. 하지만 사실 수학에는 일상 속 호기심에서 비롯된 아주 재미있는 문제들이 많아요. 오늘은 그 중에서도 수학계의 유명한 난제 중 하나, 이른바 **“소파 문제(Sofa Problem)”**에 대해 소개해드릴게요. 이름부터 왠지 귀엽고 흥미롭지 않나요?
“소파 문제”란?
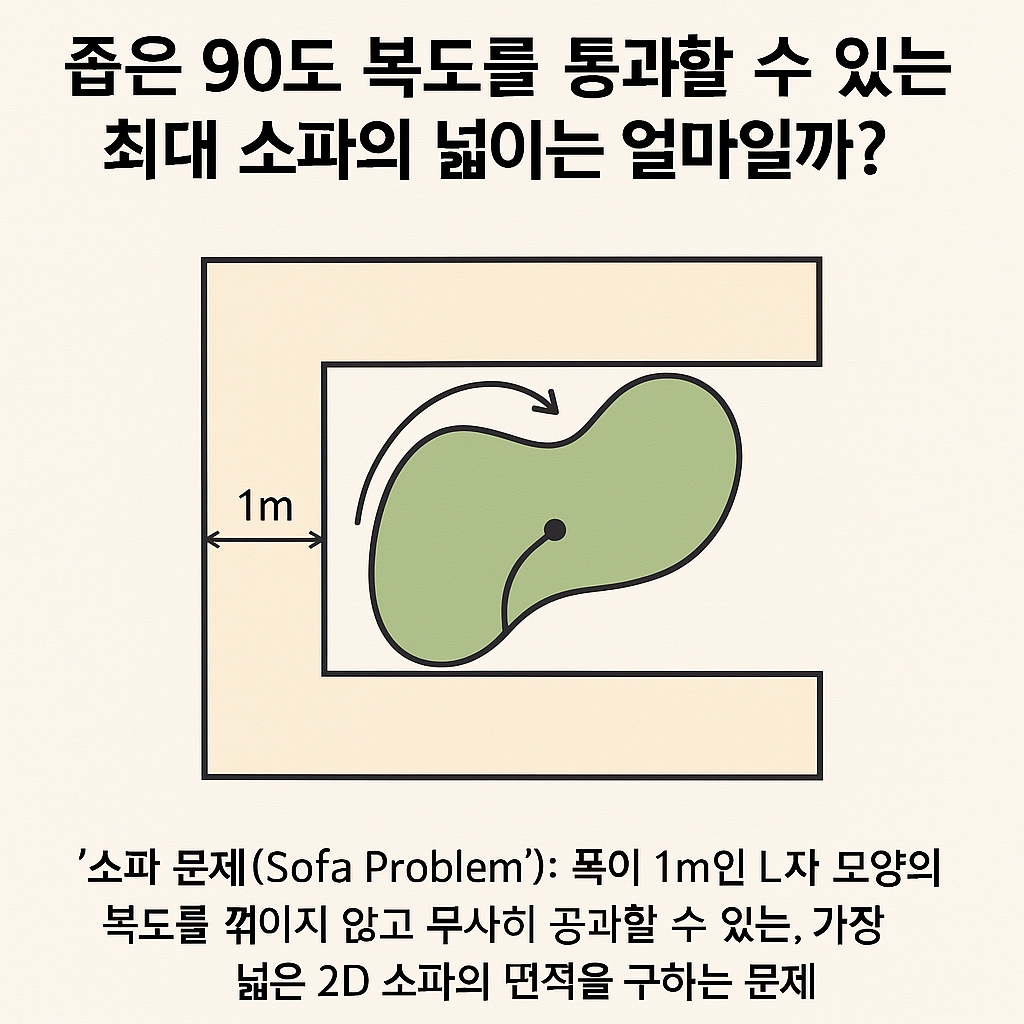
이 문제는 간단한 상상에서 출발해요.
“폭이 1m인 L자 모양의 복도를 꺾이지 않고 무사히 통과할 수 있는, 가장 넓은 2D 소파의 면적은 얼마일까?”
이 문제는 1966년 수학자 Leo Moser에 의해 처음 제기되었어요. 매우 직관적이고 현실적인 상황이지만, 그 단순한 설정과는 달리 아직까지도 정확한 정답은 알려지지 않은 미해결 문제랍니다!
여기서 조건은 이렇습니다:
• 복도는 수직으로 꺾인 L자 형태입니다.
• 복도의 너비는 항상 1입니다.
• 소파는 딱딱한 물체가 아니라 어느 정도 회전도 하고 움직일 수 있는 유연한 모양입니다.
• 단, 2차원 평면 상의 면적만 고려합니다.
즉, 이 문제는 2차원 도형이 얼마나 넓으면서도 유연하게 회전하여 L자 복도를 통과할 수 있는가를 묻는 것이죠.
왜 이게 수학 문제일까?
이 문제는 단순한 호기심에서 시작됐지만, 실제로는 기하학, 최적화 이론, 계산 기하학 등 다양한 수학 분야와 연결돼 있어요.
단순히 “넓은 도형”을 생각하는 게 아니라, 복도의 벽에 부딪히지 않으면서도 통과할 수 있도록 도형의 경계를 설계해야 하거든요.
즉, 이동 경로와 회전 각도, 도형의 형태, 넓이까지 모두 고려해야 하는 복합적인 문제입니다.
현재까지 알려진 결과들
비록 정확한 최댓값은 알려지지 않았지만, 수학자들은 다양한 시도를 통해 **하한(lower bound)**과 **상한(upper bound)**을 조금씩 좁혀왔어요.
1. Gerver의 소파 (1992)
수학자 Joseph Gerver는 1992년에 지금까지 알려진 가장 넓은 소파 도형을 제안했어요. 이 도형은 곡선 18개로 이루어진 복잡한 형태이며, 넓이는 약 2.2195입니다.
이것이 현재까지 알려진 **“가장 넓은 통과 가능한 소파”**예요.
하지만!
이것이 진짜 최댓값인지 아닌지는 아무도 모르고, 여전히 더 넓은 소파가 존재할 수도 있어요.
2. 상한: 2.8284
한편, 어떤 도형이든 절대로 넘을 수 없는 최대 넓이의 상한도 존재합니다.
현재까지 계산된 상한은 약 2.8284입니다. (이는 \pi / 2 + 2 / \pi에 기반한 수치예요.)
즉, 어떤 도형이든 넓이가 이 수치를 넘는다면 절대로 복도를 통과할 수 없다는 뜻이죠.
재미있는 변형: 이동식 소파 문제 (Moving Sofa Problem)
우리가 지금까지 이야기한 소파 문제는 이동은 하되 복도의 구조는 고정된 상황을 가정했어요.
하지만 이 문제의 변형 버전인 **“회전 소파 문제(Rotating Sofa Problem)”**도 있답니다.
또 다른 흥미로운 버전은 복도의 구조 자체가 움직이는 경우, 즉 복도 벽이 회전할 수 있을 때 가장 넓은 소파는 무엇인가? 하는 문제예요. 이런 변형 문제들도 함께 연구되고 있지만, 원래 문제만큼이나 어려운 상황이죠.
수학적 유산과 문화적 파급력
이 문제는 너무나도 직관적이고 상상하기 쉬워서, 단순한 수학 문제를 넘어서 다양한 분야에서 회자되고 있어요.
• 컴퓨터 그래픽 분야에서는 로봇이나 물체가 좁은 공간을 통과할 수 있는 경로를 찾는 알고리즘 개발에도 응용되고 있고요,
• 예술, 디자인 분야에서는 소파 문제에서 영감을 얻은 작품들이 전시되기도 해요.
• 또, 몇몇 게임이나 퍼즐에서도 이 문제를 응용한 레벨이 등장하기도 하죠!
마치며: 수학은 삶의 곳곳에
“소파 문제”는 단순한 수학 문제를 넘어서, 일상적인 상상 속에서도 수학의 깊은 원리가 숨어 있다는 것을 잘 보여주는 예입니다.
복잡한 공식이 없어도 누구나 이해할 수 있고, 누구나 “혹시 내가 더 좋은 소파를 생각해낼 수 있을까?”라고 상상해볼 수 있다는 점에서 참 매력적이죠.
혹시 여러분도 지금, 마음속으로 소파 도형을 그리고 계신가요?
여러분의 상상 속 소파가 Gerver 소파보다 더 넓을지도 몰라요!
⸻
'Ji._.INFO' 카테고리의 다른 글
| [봄 제철 식재료] 향긋한 봄내음 가득한 '냉이' 이야기와 요리법 정리 (0) | 2025.03.27 |
|---|---|
| 60년 난제를 푼 한국 수학자, 백진언 연구원과 ‘소파 문제’의 기적 같은 해답 (0) | 2025.03.27 |
| 위키드(Wicked) 줄거리·등장인물·관람 포인트 총정리! (0) | 2025.03.24 |
| [뮤지컬 리뷰] 알라딘 뮤지컬 줄거리 총정리! 환상적인 무대 마법 속으로 (0) | 2025.03.24 |
| 대만의 대표적인 아침 식사, 탄삥(蛋餅) (0) | 2025.03.23 |



